This page contains a list of problems for this year. All previous problems can be found at ipt.science/archive.
Prologue
There is no uniquely favored understanding of a problem’s conditions and it is up to each team to interpret the conditions in a way that is both interesting from a physical perspective and coherent with the problem statement. It is assumed that every phenomenon will be studied with the aim of proposing and validating a model that explains the phenomenon and its dependence on the most relevant parameters. All experiments should comply with local safety regulations and care should be exercised when dealing with dangerous equipment and substances. Whenever an experiment is not possible because of safety concerns or monetary reasons the teams are encouraged to perform an analogue experiment if possible. Teams are solely responsible for any damage or injuries incurred while working (or thinking) on the problems.
We welcome suggestions for new problems - watch out for curious everyday phenomena, intriguing demos, and write to our suggestions form. The full list of submitted problems at the submission deadline (usually June) is carefully worked through by our problem committee, and then the shortlist is voted by the entire IPT community through the national representatives.
1. String Telephone
Build a string telephone without any electronics and analyze the transmission properties (e.g. bandwidth, signal to noise ratio, etc.) of the device. Maximize the distance over which this device allows you to speak. Can you modify the device to make a group call?
2. The Life of Beer Foam
Investigate the dynamics of beer foam (or the foam of any equivalent non-alcoholic drink) after pouring. Study and characterize the relevant parameters of the foam evolution. Maximize the lifetime of the foam per unit volume of beer.
3. Ping-Pong Balls Cannon
Construct a mechanical cannon (no explosives or compressed gas) capable of launching a ping pong ball a considerable distance without breaking it. Optimize the design to maximize the distance reached by the ping-pong balls. Discuss the distance vs. precision trade-off. Take extreme care when performing these experiments.
4. Periodic Gurgles
Turn an open bottle of water, juice, lemonade, ketchup, or shampoo upside down. Rather than flowing continuously, the liquid comes out in periodic gurgles. Investigate the phenomenon. How do results change if the bottle is tilted?
5. Electrostatic Cyclotron
Using a DC voltage source and a plastic ball covered in aluminum foil, build the setup shown in the video. Determine under which conditions the setup can work and maximize the ball’s speed.
https://www.youtube.com/shorts/t6uECHfaxgs
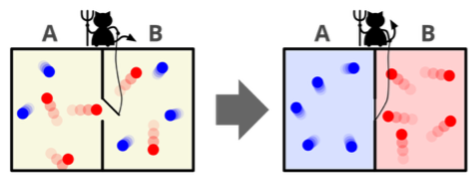
6. Maxwell’s Demon
The Maxwell’s demon thought experiment is a famous setup in which one is able to create a temperature differential in an initially thermalized gas by exploiting the information extracted from measurements on the gas particles. There are many versions of the setup that fundamentally show the same thing (e.g. creating a difference in number of particles instead of temperature).
By placing a shallow box with small balls inside on a vibrating table one can simulate a 2D gas in a box. Implement the Maxwell Demon setup in such a system (or one of its cousins) and optimize the speed and efficiency of the process by which you create the difference in thermodynamic potential. Furthermore, is it possible to turn your device into an engine and use perform work? If so, characterize its power and power fluctuations.
Hint: By using balls of different masses one can simulate a gas with different chemical species.
7. Double Decker Newton’s Cradle
Make a double decker Newton’s cradle (as in the video) and explain the phenomenon. Optimize the transmission of the kinetic energy between the levels. How does the number of balls per layer change the transmission efficiency?
8. Eddy Current Engine
Make an Eddy current engine, with an AC voltage source and aluminum discs as in the video. Explain the phenomena, maximize the angular velocity of the discs, and maximize the efficiency of this engine.
https://www.youtube.com/shorts/TVdB5-UKN8s
9. Water “Laser”
A shallow water tank mechanically excited by a motor features some of the basic ingredients of a laser (i.e. a cavity and an amplifier). To what extent can this simple analogy capture more complex aspects of laser physics, such as spontaneous and stimulated emission, population inversion, Q switching, and others?
10. Dancing Soapy Vortices
When exposed to sound, a soap film shows beautiful dancing color patterns. Under certain conditions, vortices appear on the film surface. Investigate the phenomena. What are the best conditions for them to appear (e.g. sound frequency, incident angle of the sound waves, size of the film, etc.)?
https://www.youtube.com/shorts/j9Y3ansvt0U
11. Cosmic Skyscraper Tomography
Radiography is an imaging technique that uses X-rays, gamma rays, or similar ionizing radiation and non-ionizing radiation to view the shape of an object. There also exist many methods of using cosmic rays in tomography of terrestrial objects, such as muography. Develop a similar method that will allow you to determine how many floors are above you in the building where you place the experiment. How does the accuracy of your method depend on the relevant parameters?
12. Kinetic Voltmeter
A DIY method of testing the charge of a battery is to drop it on a hard surface and observe whether it bounces. Explain the phenomenon and find other non-invasive mechanical methods to estimate the remaining charge. Optimize the accuracy of your method. https://www.youtube.com/watch?v=suH32X91sQE
13. Rice Holes
If you do the rice cooking without ever stirring it, you will find out that your well-cooked and tasty rice shows a pattern of holes like the one in the picture. Can you suggest a physical explanation for the phenomenon? Identify the relevant parameters.

14. Kaleidoscope Tomography
A kaleidoscope is an interesting device that uses a set of mirrors to construct fascinating geometric patterns. Using a coherent light source and diffraction elements on one end, and a camera on the other end, reconstruct the internal structure of the kaleidoscope.
15. Singing Water
Several cultures use water as a musical instrument, creating a variety of sounds depending on how the surface of the water is stroked. Explain how the sound is formed and investigate how the properties of the sound depend on the stroke technique. https://youtu.be/i5ECtJvKd94
16. Singing Flame
It is now well known that flames can travel. However, did you know that they can sing too? They will emit sound if an alternating electrical current passes through them. Explain this phenomenon and identify the relevant parameters. Find a way to record sounds with the flame. Characterize the spectral response function of your device and optimize it to have the highest sound fidelity. https://www.youtube.com/watch?v=2ZJ8SF3BnNw
17. Crazy Cylinder
Fill the space between two parallel panels with liquid, then attach two threads to the ends of a heavy circular cylinder and submerge it into the liquid. The cylinder diameter should be slightly smaller than the inter-panel distance. Next, pull the cylinder up, and under some circumstances the cylinder will begin to hit the walls periodically. Explain this phenomenon. Identify the conditions for the oscillations to occur. What is the oscillation frequency and how does it depend on relevant parameters? What changes if the liquid is non-Newtonian?
Preselection problems
The preselection problems are 1. String Telephone 12. Kinetic Voltmeter and 16. Singing Flame for everyone.
The countries that have a national selection can also choose from the additional two problems 8. Eddy Current Engine and 17. Crazy Cyclinder.
